Iterative Closest Point. More...
#include <Icp.hpp>
 Inheritance diagram for TRTK::IcpInterface< ValueType >:
Inheritance diagram for TRTK::IcpInterface< ValueType >:Public Types | |
|
typedef Eigen::Matrix < ValueType, Eigen::Dynamic, Eigen::Dynamic > | Matrix |
Public Member Functions | |
| virtual void | setSourcePoints (const std::vector< Coordinate< ValueType > > &source_points)=0 |
| Set the data points as decribed above. | |
| virtual void | setTargetPoints (const std::vector< Coordinate< ValueType > > &target_points)=0 |
| Set the model points as decribed above. | |
| virtual void | setInitialEstimation (const Matrix &transformation)=0 |
| Set the initial transformation from the source to the target point coordinate system. | |
| virtual void | setEstimationAlgorithm (EstimateTransformation3D< ValueType > &estimator)=0 |
| Set the transformation estimator. | |
| virtual void | setMaximumNumberIterations (unsigned number)=0 |
| Set the maximum number of iterations performed by an algorithm (default is 20). | |
| virtual void | setMaximumRMSE (ValueType value)=0 |
| Set an upper bound of the root mean square error; an algorithm terminates if the error of the current estimation falls below this value (default is 0). | |
| virtual void | setEpsApproximate (float value)=0 |
| Set the value for the eps-approximate neighbor search. The higher the value the faster the search (but also the less accurate) (default is 0). | |
| virtual ValueType | compute ()=0 |
| Call this function to perform the transformation estimation. The RMSE is returned. | |
| virtual void | abortComputation ()=0 |
| Call this function to abort a running algorithm. | |
| virtual const Matrix & | getTransformation ()=0 |
| Returns the estimated transformation in the form of a homogeneous matrix. | |
Iterative Closest Point.
| ValueType | Scalar type (must be a floating point type). |
The iterative closest point (ICP) algorithm allows solving a registration problem where some data points (source points) shall be geometrically aligned with a given model. The model is also given by a set of points (target points).
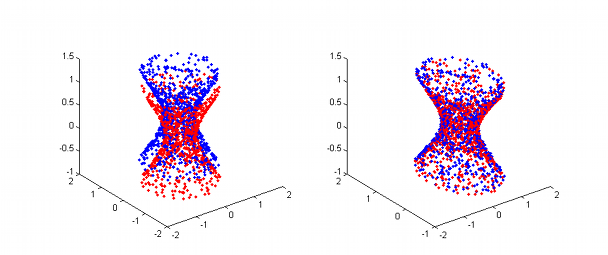
Left: Model points (blue) and unaligned data points (red). Right: Registered with the ICP algorithm.
This header file contains several variants of the ICP algorithm, first and foremost the original algorithm of Chen and Medioni [1] or Besl and McKay [2] for 2D and 3D point clouds.
The general concept of the ICP algorithm is always as follows:
Given some model and data points and an initial transformation between both point sets (from the data coordinate system to the model coordinate system)
Internally the query for point correspondencies is done using an approximate nearest neighbor search which can significantly improve the query time. By default no approximation is done (eps-approximate of zero). To do an approximate search, set the eps value to a value greater than zero using the function setEpsApproximate(). Note, the search structure is only built up from the set of target points which is assumed to be bigger than the set of data points.
The transformation estimator can be an arbitrary estimator. See EstimateTransformation and its subclasses for more details.
The current state of computation is provided by the signal progress. The computation can be canceled at each point in time by calling the function abortComputation().
Example:
In the following example, the point clouds seen in the figure above are registered. Each of the clouds consists of points lying on the surface of a hyperboloid. The blue points are the undistorted model points, the red ones are the noisy data points which shall be aligned with the model points.
First, we will construct these two point sets. Then we will set an initial transformation estimation and finally we will run the ICP algorithm and put out the results.
#include <iostream> #include <TRTK/Icp.hpp> #include <TRTK/EstimateRigidTransformation3D.hpp> #include <TRTK/Tools.hpp> #include <TRTK/Transform3D.hpp> using namespace std; using namespace TRTK; using namespace TRTK::Tools; void printProgress(unsigned value) { cout << "Progress: " << value << endl; } int main() { typedef Coordinate<double> Point; typedef vector<Point> Points; typedef TRTK::Icp3D<double> ICP; double pi = 3.1416; // Generate some model points. Points target_points; unsigned number_target_points = 1000; target_points.reserve(number_target_points); for (unsigned i = 0; i < number_target_points; ++i) { // points lying on the surface of a hyperboloid double s = rand<double>(-1.0, 1.0); double t = rand<double>() * 2 * pi; double x = sqrt(s * s + 0.2) * cos(t); double y = sqrt(s * s + 0.2) * sin(t); double z = s; target_points.push_back(Point(x, y, z)); } // Generate some noisy data points. These points shall also be unaligned // with the model points. Transform3D<double> transform; transform.rotateAxis(10.0 / 180.0 * pi, Point(1, 1, 10)).translate(0.1, 0.2, 0.3); Points source_points; unsigned number_source_points = 1000; source_points.reserve(number_source_points); for (unsigned i = 0; i < number_source_points; ++i) { double s = rand<double>(-1.0, 1.0); double t = rand<double>() * 2 * pi; double x = sqrt(s * s + 0.2) * cos(t); double y = sqrt(s * s + 0.2) * sin(t); double z = s; Point source_point = transform * Point(x, y, z); // displace source_point += sigma * Point(randn(), randn(), randn()); // add noise source_points.push_back(source_point); } // Set an initial transformation estimation (pre-registration). ICP::Matrix initial_transformation = Eigen::Matrix4d::Identity(); // Register the two point sets using a rigid transformation. EstimateRigidTransformation3D<double> estimator; ICP icp; icp.setSourcePoints(source_points); icp.setTargetPoints(target_points); icp.setInitialEstimation(initial_transformation); // by default identity icp.setEstimationAlgorithm(estimator); icp.setMaximumNumberIterations(10); icp.setMaximumRMSE(0.07); icp.progress.connect(&printProgress); cout << "Start computation.\n"; double rmse = icp.compute(); cout << endl << "The RMSE is " << rmse << endl << "and the sought transformation is:" << endl << icp.getTransformationMatrix(); return 0; }
Output:
...
[1] Yang Chen and Gerard Medioni, "Object Modelling by Registration of Multiple Range Images", Image and Vision Computing, 1991
[2] Paul J. Besl and Neil D. McKay, "A Method for Registration of 3-D Shapes", IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992
[3] Rusinkiewicz and Levoy, "Efficient Variants of the ICP Algorithm", International Conference on 3-D Digital Imaging and Modeling, 2001
Definition at line 227 of file Icp.hpp.
Documentation generated by Doxygen